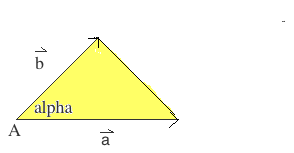
Vektorielle Flächenformel Dreieck Raum:
Vektorielle Flächenformel:
Die vektorielle Flächenformel beruht auf folgenden Voraussetzungen:
– Ein Dreieck ist durch 2 Vektoren aufgespannt.
– Die trigonometrische Flächeninhaltsformel für das Dreieck lautet: A = 1/2 * | | * |
| * | | * sin α
| * sin α
Formel:
A = 1/2 * √( ² *
² *  ² - (
² - ( *
*  )²)
)²)
Beispiel:
gegeben: Dreieck mit den Richtungsvektoren und
gesucht: Flächeninhalt

Lösung:
A = 1/2 * √(² *
² – (
*
)²)
A = 1/2 * √(35 * 26 – 26²)
A = 1/2 * √234
A = 7,65 FE
A: Der Flächeninhalt des Dreiecks beträgt 7,65 FE.
Nebenrechnungen: