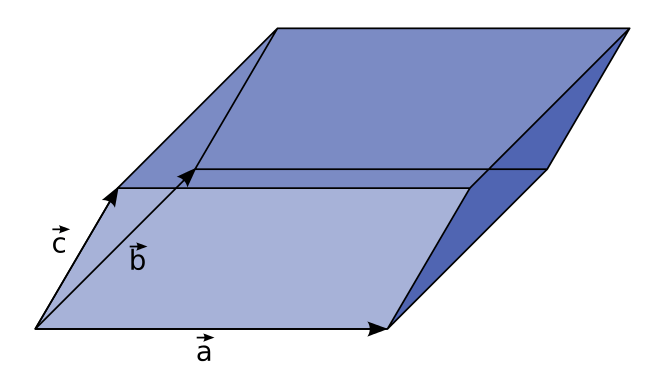
Vektoren Parallelepiped Volumen:
Überblick Parallelepiped:
In anderen Worten handelt es sich beim Parallelepiped um einen geometrischen Körper, der von sechs paarweise kongruenten in parallelen Ebenen liegenden Parallelogrammen begrenzt wird.
Das Parallelepiped hat 12 Kanten, von denen jeweils 4 gleich lang sind und besitzt 8 Ecken.
Der rechteckige Quader (sechs rechteckige Flächen), der Würfel (sechs quadratische Flächen) und das Rhomboeder (sechs Rautenflächen ) sind spezielle Fälle des Parallelepipeds.
Da die Kristalle des Kalkspats die Form eines Parallelepipeds aufweisen wird er auch Spat genannt.
Formel für Volumensberechnung:
Bestandteile:
= Richtungsvektor
= Richtungsvektor
= Richtungsvektor
Beispiel:
gegeben: Parallelepiped mit den Richtungsvektoren ,
und
gesucht: Volumen
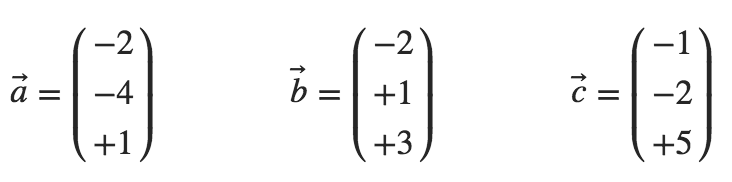

V = | x
*
|
V = | – 45|
V = 45 VE
Nebenrechnung:
x
*
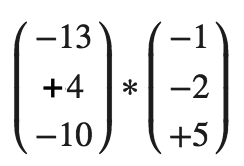
(-13) * (-1) + (+4) * (-2) + (-10) * 5 =
+ 13 – 8 – 50 = – 45
A: Das Volumen des Parallelepiped beträgt 45 VE.
Übungen:
Parallelepiped Volumen Übung 1 Lösung
Gegeben ist das Parallelepiped:
ABCDEFGH [A (-4/2/-5), B (4/-2/-3), D (1/3/-2), E (-3/-5/13)]
Berechne das Volumen des Parallelepipeds
Parallelepiped Volumen und Höhe Übung 2 Lösung
Gegeben ist das Parallelepiped:
[A (0/0/2), B (4/3/5), D (4/-1/-1), E (-5/6/7)]
Berechne Berechne das Volumen und die Höhe des Parallelepipeds
Übungsblätter:
Parallelepiped Volumen Übungsblatt