Vektor-Winkel-Formel im Raum:
Mit der Vektor-Winkel-Formel können Winkel zwischen zwei Vektoren berechnet werden.
Berechnung:
Der Zähler ist das skalare Produkt der beiden Richtungsvektoren 
und 
.
und 
.Der Nenner ist das Produkt der beiden Beträge der Richtungsvektoren || * ||.
| * ||.Gesucht ist immer der spitze Winkel.
Ergibt sich als Lösung ein stumpfer Winkel, so wird der Supplementärwinkel als Lösung angegeben: ρ´= 180° – ρ
Formel:
cos ρ = *
* || * ||
| * || cos ρ = Vektorwinkel
= Richtungsvektor = Richtungsvektor || = Betrag/Länge vom Richtungsvektor
| = Betrag/Länge vom Richtungsvektor|| = Betrag/Länge vom Richtungsvektor
| = Betrag/Länge vom Richtungsvektor
Vektor-Winkel-Formel im Raum Beispiel:
Berechne den Winkel, den die beiden Vektoren und einschließen:
und einschließen:
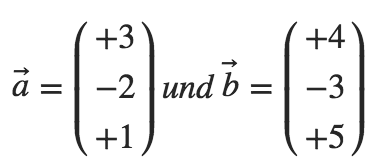
Lösung:
cos ρ = *
* || * ||
| * ||
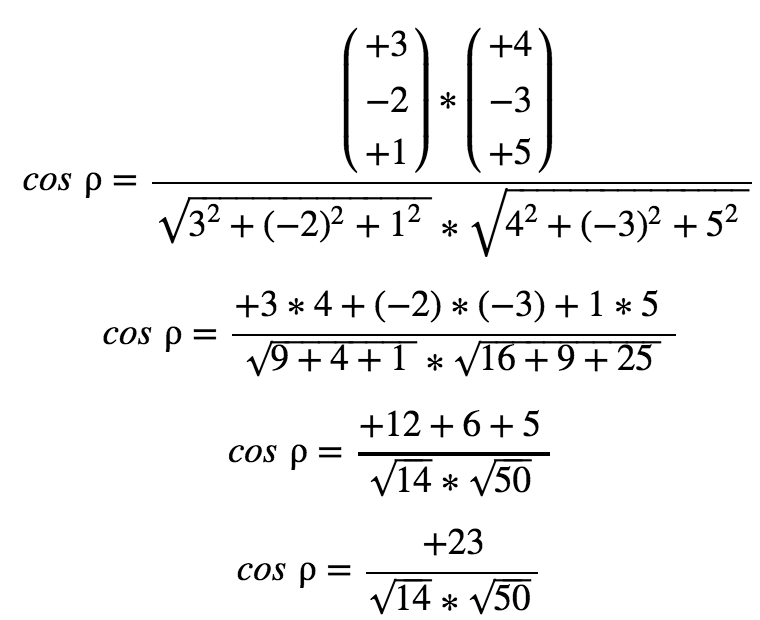
cos ρ = 0,869… cos-1
Taschenrechner = 29,62°
Übungsblätter:
Vektor-Winkel-Formel im Raum Merkblatt