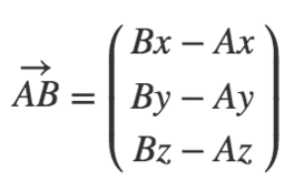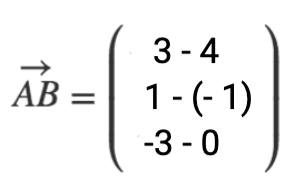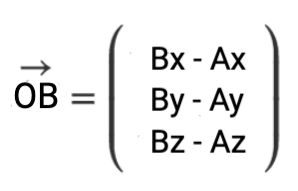Spitze minus Schaft Formel im Raum:
Die Koordinaten eines Vektors ergeben sich aus der Differenz der Koordinaten des Endpunkts (Spitze) und Anfangspunkt (Schaft).
Deshalb wird diese Berechnung “Spitze minus Schaft Formel” genannt.
Anders formuliert kann man mit dieser Formel aus zwei Punkten einen Vektor berechnen, indem man von zwei Ortsvektoren jeweils die Differenz der Koordinaten berechnet.
Vorgangsweise:
Im 1. Schritt wird vom x-Wert des Endpunktes (Spitze) der x-Wert des Anfangspunktes (Schaft) subtrahiert.
Im 2. Schritt wird vom y-Wert des Endpunktes (Spitze) der y-Wert des Anfangspunktes (Schaft) subtrahiert.
Im 3. Schritt wird vom z-Wert des Endpunktes (Spitze) der z-Wert des Anfangspunktes (Schaft) subtrahiert.
Beispiel: Richtungsvektor 
gegeben: Punkte: A (4/-1/0) und B (3/1/-3)
gesucht: der Vektor (Richtungsvektor)
Berechnung mit Spitze minus Schaft Formel:
| |
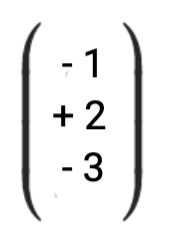 |
Beispiel: Ortsvektor 
gegeben: Punkte: A (4/-1/0) und B (3/1/-3) sowie der Ursprung mit (0/0/0)
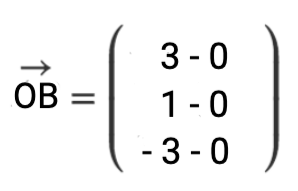
| |
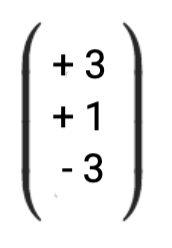 |
PDF-Übungsblätter:
Spitze minus Schaft Formel im Raum Merkblatt
Spitze minus Schaft Raum Übungsblatt
Spitze minus Schaft Raum Ortsvektor Übungsblatt