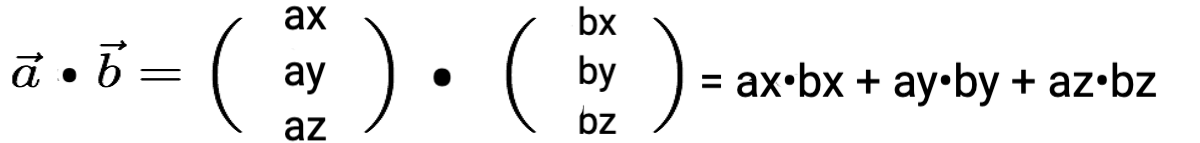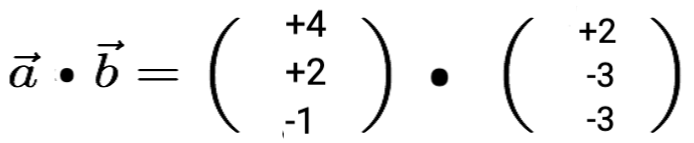Skalaresprodukt im Raum:
Werden zwei Vektoren miteinander multipliziert, ist das Ergebnis ein Skalar (eine reelle Zahl).
Dabei werden die jeweiligen x-, y- und z-Koordinaten miteinander multipliziert und von den Ergebnissen wird eine Summe gebildet.
Formel:
Beispiel:
wenn = (4/2/-1) und
= (2/-3/-5)
Berechnung:
4 • 2 + 2 • (- 3) + (-1) • (-3) =
8 – 6 + 3 = + 5
Das Ergebnis der skalaren Multiplikation zweier Vektoren ist eine reelle Zahl.
Rechengesetze:
Für drei Vektoren ,
und
∈ ℝ gilt:
a) Kommutativgesetz (Vertauschungsgesetz): •
=
•
b) Distributivgesetz (Verteilungsgesetz): • (
+
) =
•
+
•
und ( +
) •
=
•
+
•
c) Skalarprodukt eines Vektors mit sich selbst ergibt das Quadrat seiner Länge: •
= a²
d) Sind und
orthogonal, so gilt:
•
= 0
Orthogonalitätsbedingung:
Zwei Vektoren sind dann orthogonal (stehen normal aufeinander), wenn ihr skalares Produkt 0 ist!
steht normal auf
wenn
•
= 0
PDF-Übungsblätter:
Skalarprodukt Aufgaben Übungsblatt
Skalarprodukt im Raum Übungsblatt
Skalarprodukt Rechengesetze Übungsblatt