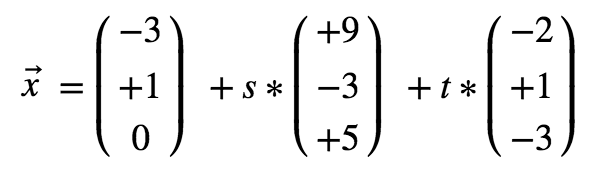Parameterdarstellung im Raum:
Jeder Punkt (Ortsvektor ) einer Ebene ε ist durch eine Vektoraddition darstellbar, indem zu einem bestehenden Ausgangspunkt
1 das Vielfache (Parameter s und t) der beiden Richtungsvektoren
und
addiert wird.
Anders formuliert, wird die Ebene durch zwei Richtungsvektoren ( und
), die nicht parallel sind, von einem gegebenen Ausgangspunkt
1 aufgespannt.

Formel:
ε: =
1 + s •
+ t •
s, t ∈ ℝ
Erklärung:
= Ortsvektor aller Punkte X der Ebene
1 = gegebener Ausgangspunkt
,
= Richtungsvektoren
s, t = Parameter
Beispiel:
gegeben: A (-3/+1/0), B (6/-2/5) und C (-5/2/3)
gesucht: Parameterdarstellung der Ebene in Vektorform
1. Schritt: Bildung der Richtungsvektoren und
Bilde mit der Spitze minus Schaft Formeln die Richtungsvektor und
mit A (-3/+1/0), B (6/-2/5) und C (-5/2/3)
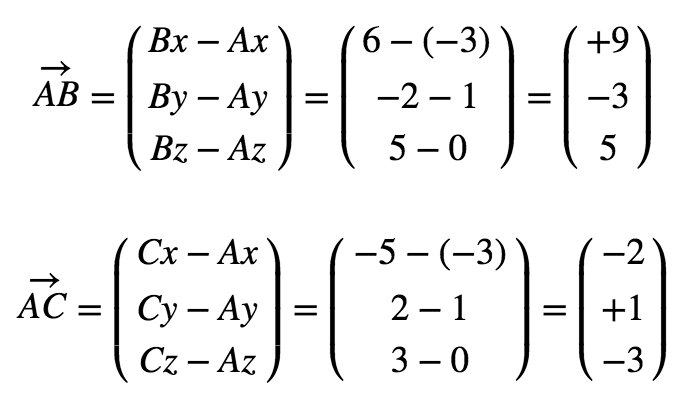
2. Schritt: Parameterdarstellung:
Wir spannen die Ebene ausgehend vom Punkt A mit den beiden oben berechneten Richtungsvektoren und
auf
ε: =
1 + s •
+ t •
s, t ∈ ℝ
PDF-Übungsblätter
Parameterdarstellung im Raum Übungsblatt 1
Parameterdarstellung Raum Aufgaben Übungsblatt