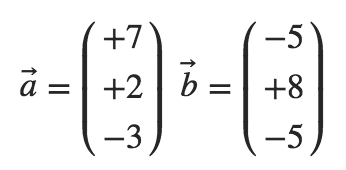Orthogonalität im Raum:
Zwei Vektoren sind genau dann orthogonal (stehen normal aufeinander), wenn ihr skalares Produkt gleich Null ist.
Beispiel von zwei orthogonalen Vektoren:
Berechne das skalare Produkt der Vektoren  und
und  , wenn
, wenn
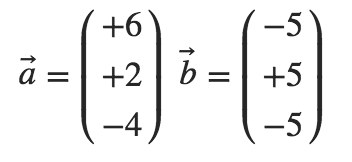
Formel:
Das Ergebnis der skalaren Multiplikation zweier Vektoren ist eine reelle Zahl.
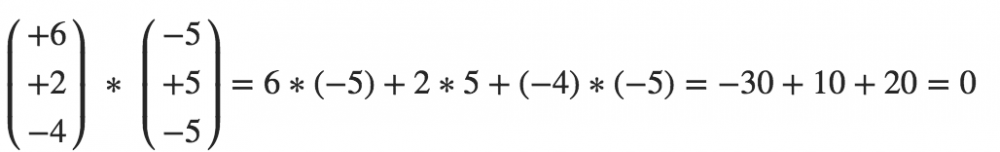
d.f. die beiden Vektoren sind orthogonal, da  *
*  ≠ 0
≠ 0
Beispiel von zwei nicht orthogonalen Vektoren:
Berechne das skalare Produkt der Vektoren und
, wenn
Formel:
Das Ergebnis der skalaren Multiplikation zweier Vektoren ist eine reelle Zahl.
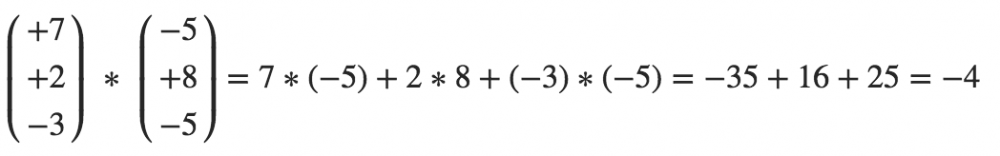
d.f. die beiden Vektoren sind nicht orthogonal, da  *
*  ≠ 0
≠ 0