Normalvektorform im Raum:
Mithilfe der Normalvektorgleichung ermitteln wir die Konstante der Normalvektorform im Raum.
Dazu benötigen wir einen Normalvektor 
und einen Ortsvektor 
1
und einen Ortsvektor 
1Formel:
ε: * = * 1
* = * 1 = Normalvektor = Variablenvektor1 = OrtsvektorHerleitung der Formel:
Die Normalvektorform der Ebene wird aus der Parameterform der Ebene abgeleitet.
Durch die Multiplikation mit dem Normalvektor fallen die Parameter s und t weg,
fallen die Parameter s und t weg, da 
* = 0 und 
* = 0
* = 0 und 
* = 0 = 1 + s * + t * / *
* = * 1 + s * * + t * *
* = * 1 + 0 + 0
* = *
Beispiel:
gesucht: Normalvektorform der Gleichung
gegeben: Normalvektor und Ortsvektor 
:
und Ortsvektor 
:
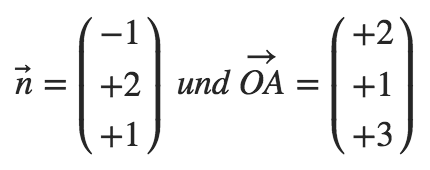
Lösung:
ε: * = * 1
Anmerkung: Werden 2 Vektoren miteinander multipliziert, ist das Ergebnis ein Skalar.
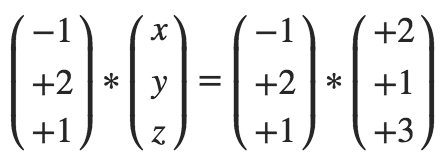
– x + 2y + z = – 1 * 2 + 2 * 1 + 1 * 3
– x + 2y + z = – 2 + 2 + 3
– x + 2y + z = +3