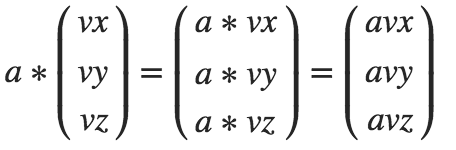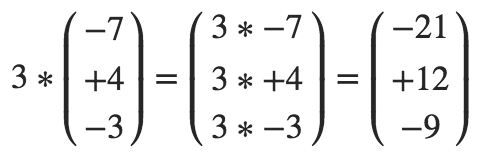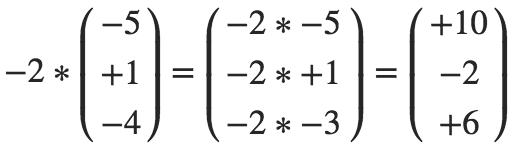Multiplikation Skalar und Vektor im Raum:
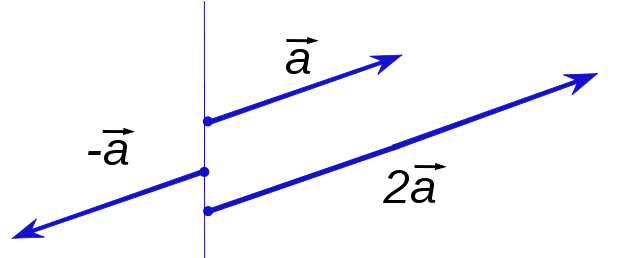
Wird eine Verschiebung eines Vektors (Addition) mehrfach hintereinander durchgeführt, so kann dies mit einer Multiplikation vereinfacht werden (hier * 2).
Ist der Skalar negativ (hier * -1) , ändert sich die Richtung des Vektors.
Grundformel:
Bei der Multiplikation einer Zahl (Skalar) mit einem Vektor, wird jede Vektorkomponente mit der Zahl multipliziert.
Beispiele:
Multiplikation eines Skalars mit einem Vektor im Raum
Multiplikation des Vektors mit einem negativen Skalar: