Kurvendiskussion:

Geometrische Eigenschaften:
– Schnittpunkte mit den Koordinatenachsen (z.B. Nullstellen)
– Hoch- und Tiefpunkte (z.B. lokale Extremstellen)
– Wendepunkte und Wendetangenten
– Asymptoten
– Monotonie- und Krümmungsverhalten, etc.
Definitionsbereich einer Funktion:
Der Definitionsbereich einer Funktion ist die Menge der reellen Zahlen, die für die Variable x eingesetzt werden können.
Geometrisch sind es alle Zahlen der x-Achse (x-Werte), für die ein y-Wert berechnet werden kann.
Beispiele:
a) Lineare Funktion:
f (x) = x + 3 → Definitionsbereich -∞ bis +∞
Anmerkung: Lineare Funktionen sind in der gesamten Menge der reellen Zahlen definiert.
b) Quadratische Funktion:
f (x) = x² + 2x + 3 → Definitionsbereich -∞ bis +∞
Anmerkung: Quadratische Funktionen sind in der gesamten Menge der reellen Zahlen definiert.
c) Quadratwurzelfunktion:
f (x) = √(x + 3) → Definitionsbereich -3 bis +∞
Anmerkung: Der Wert unter der Wurzel darf nicht negativ sein.
Wertebereich einer Funktion:
Der Wertebereich einer Funktion besteht aus der Menge der reellen Zahlen, die man beim Einsetzen der x-Werte erhält → f (x) bzw. y-Werte.
Beispiele:
a) Lineare Funktion:
f (x) = x + 3 → Wertebereich -∞ bis +∞
Anmerkung: Der Wertebereich einer linearen Funktion ist für die gesamte Menge der reellen Zahlen definiert.
b) Quadratische Funktion:
f (x) = x² + 2x + 3 → Wertebereich 2 bis +∞
Anmerkung: Der y-Wert kann nicht kleiner werden wie y des Scheitelpunktes.
c) Quadratwurzelfunktion:
f (x) = √(x + 3) → Wertebereich 0 bis +∞
Anmerkung: Der y-Wert einer Quadratwurzelfunktion kann nicht negativ sein.
Graph der Funktion:
Unter dem Graph einer Funktion verstehen wir die zeichnerische Darstellung im ebenen rechtwinkligen Koordinatensystem, welches in vier Quadranten aufgeteilt ist.
1. Quadrant: x-Werte positiv und y-Werte positiv z.B. (+3/+4)
2. Quadrant: x-Werte negativ und y-Werte positiv z.B. (-3/+4)
3. Quadrant: x-Werte negativ und y-Werte negativ z.B. (-3/-4)
4. Quadrant: x-Werte positiv und y-Werte negativ z.B. (+3/-4)
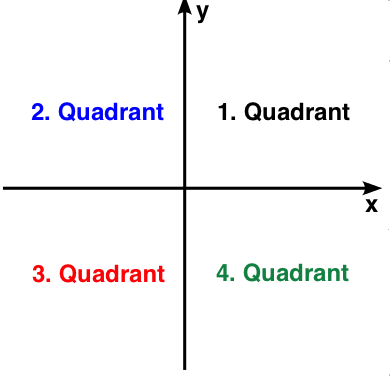
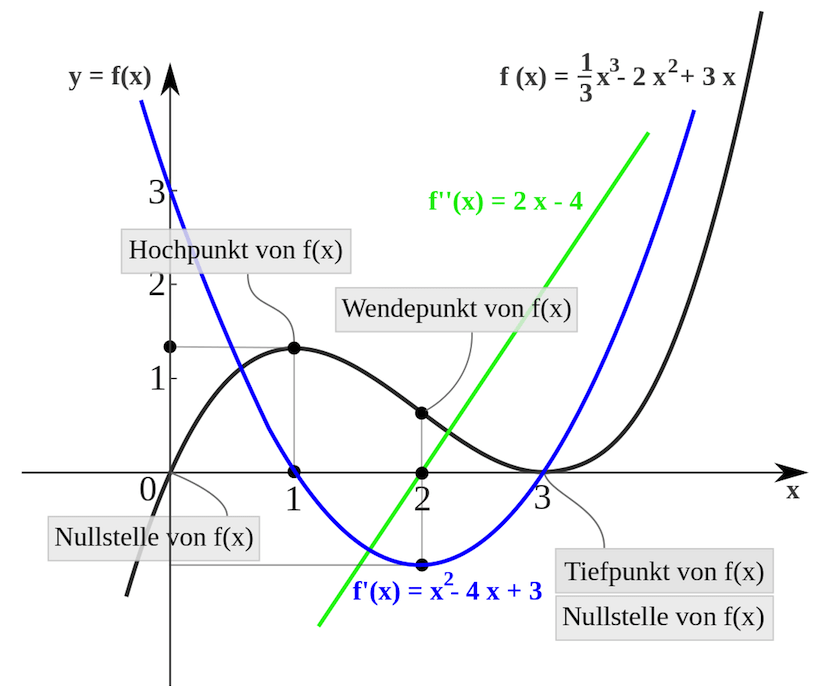 Abb. Wikipedia
Abb. WikipediaNullstellen:
Unter Nullstellen versteht man Argumente (x-Werte), die eingesetzt in der Funktion den Funktionswert (y-Wert) Null ergeben.
Bei reellen Funktionen sind das diejenigen Stellen an denen der Graph die x-Achse entweder berührt oder schneidet.
Wir unterscheiden folgende Möglichkeiten:
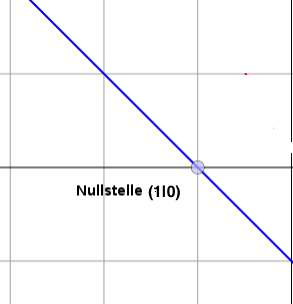
a) einfache Nullstelle
Vorkommen: lineare Funktionen
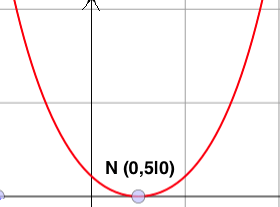
>b) doppelte Nullstellen:
Vorkommen: quadratische Funktionen (Parabeln)
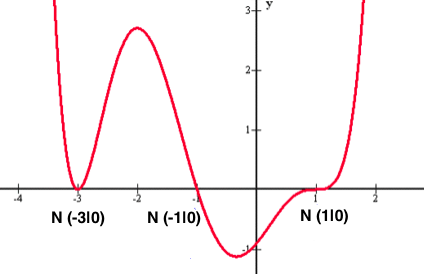
c) mehrfache Nullstellen:
Vorkommen: polynome Funktionen
Man setzt die Funktion gleich 0 und löst die Gleichung nach x auf.
Berechnung: f (x) = 0
Methoden der Berechnung: pq-Formel, Herausheben, Mitternachtsformel, Horner-Schema, Newton-Verfahren etc.
Produkte werden in Faktoren aufgeteilt und diese werden jeweils gleich Null gesetzt.
Ist eine Nullstelle (x0) bekannt, kann diese in eine Polynomdivision eingesetzt werden (x – x0), um eine Gleichung zu erhalten, die um einen Grad niedriger ist. Damit können die restlichen Nullstellen besser bestimmt werden.
Extremstellen (Hochpunkte und Tiefpunkte):
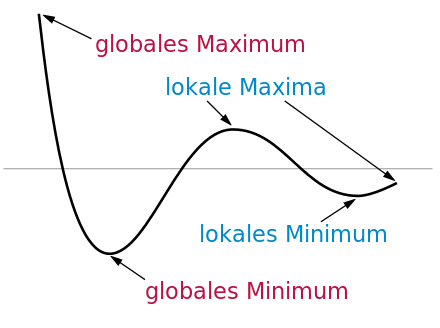 Abb. Wikipedia
Abb. Wikipedia Hochpunkt = Vorzeichen vor der Extremstelle ein + und dahinter ein –
z.B.
| x | 0,5 | 1 | 1,5 |
| f ‘(x) | + | 0 | – |
Tiefpunkt = Vorzeichen vor der Extremstelle ein – und dahinter ein +
| x | 0,5 | 1 | 1,5 |
| f ‘(x) | – | 0 | + |
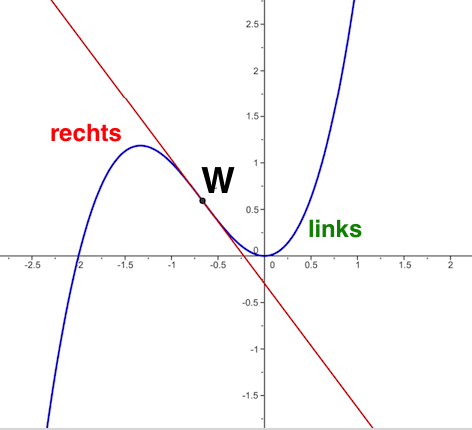
Wendepunkte:
1. Berechnung der 2. Ableitung f´´(x)
2. Nullstellen der 2. Ableitung bestimmen mit f´´ (x) = 0 ergibt Lösungen xi
3. Berechnung der 3. Ableitung f´´´ (x)
4. Bestimmung ob Wendepunkt
Nullstellen der 2. Ableitung (xi) werden in die 3. Ableitung eingesetzt
Bei f´´´(xi) ≠ 0 handelt es sich um Wendepunkte
Bei f´´´(xi) = 0 handelt es sich um Wendepunkte, wenn sich bei f´´an der Stelle xi das Vorzeichen ändert
5. Berechnung der y-Koordinate: Der xi-Wert wird in die Grundfunktion f (x) eingesetzt.
Wendetangente
Die Tangente an dem Wendepunkt P nennt man Wendetangente.
Hier handelt es sich also um eine Tangente im Wendepunkt des Graphen, die durch den Punkt P geht und die Steigung des Graphen im Punkt P hat.
Die Variablen x und y entsprechen den Koordinaten des Wendepunkts.
Die Steigung k wird berechnet indem wir x-Koordinate des Wendepunkts in die 1. Ableitung f´(xw) einsetzen.
Die Variable d erhalten wir, indem wir die Tangentengleichung auf d umformen.
Beispiel:
f´(x) = – 3/4x² + 3x, Wendepunkt W (2/4)
Symmetrieverhalten
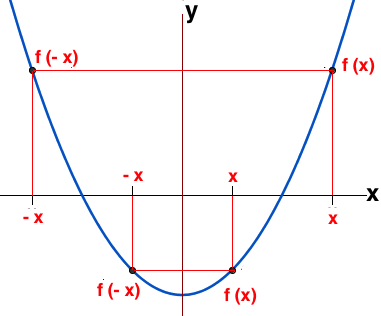
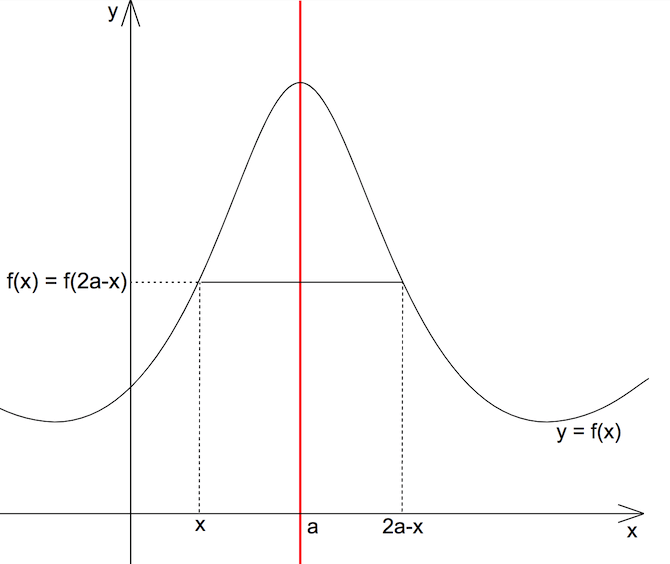
Der Graph einer Funktion f ist genau dann achsensymmetrisch zur Geraden mit der Gleichung x = a, wenn für alle x die Gleichung gilt
f (a – x) = f (a + x)
Durch Substitution von x mit x – a erhält man die äquivalente Bedingung f (2a – x) = f (x)
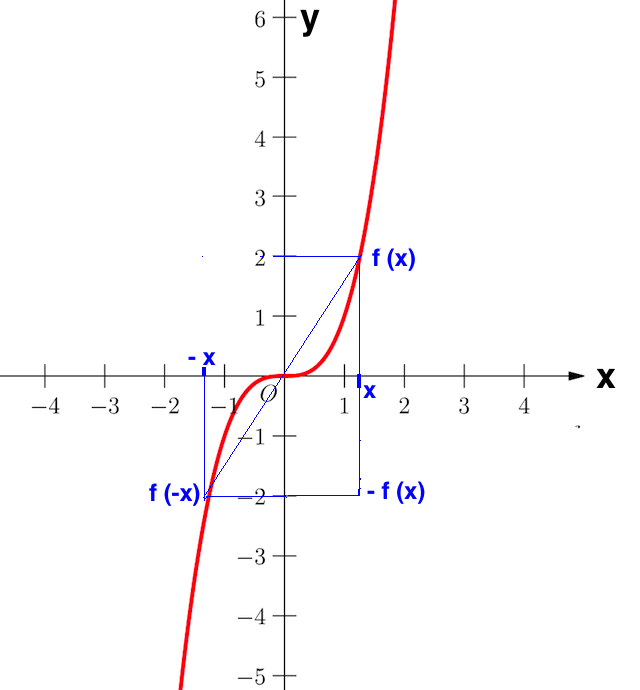
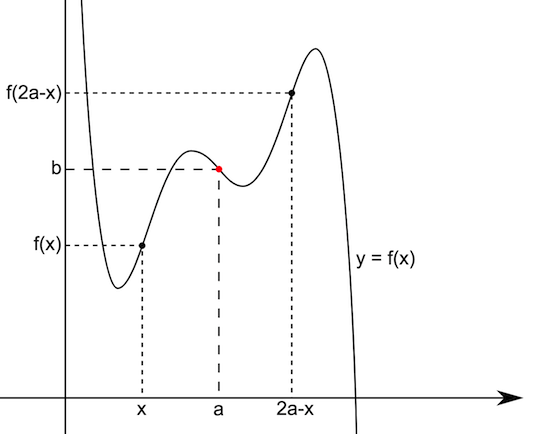
Der Graph einer Funktion f ist genau dann symmetrisch zum Punkt (a|b), wenn für alle x die Gleichung gilt
f (a + x) – b = – f (a – x) + b
Monotonieverhalten:
Definition:
Eine Funktion ist im Intervall I = [a;b] streng monoton steigend, wenn mit x1 < x2 folgt f (x1) < f (x2).
In anderen Worten, den größer werdenden x-Werte entsprechen größer werdende Funktionswerte (y-Werte).
Eine Funktion ist im Intervall I = [a;b] streng monoton fallend, wenn mit x1 < x2 folgt f (x1) > f (x2).
In anderen Worten, den größer werdenden x-Werte entsprechen kleiner werdende Funktionswerte (y-Werte).
Bestimmung:
Das Monotonieverhalten wird mithilfe der 1. Ableitung bestimmt.
Es ändert sich in den relativen Extremstellen:
f´ (x) > 0 ⇒ die Funktion f (x) ist in diesem Intervall streng monoton steigend.
f´ (x) < 0 ⇒ die Funktion f (x) ist in diesem Intervall streng monoton fallend.
Beispiel:
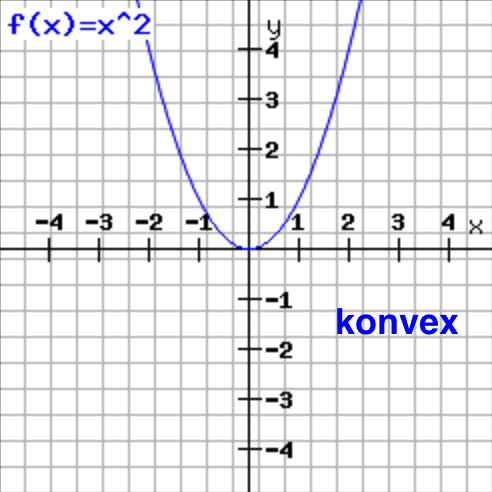
Monotonieverhalten der Funktion f (x) = x²
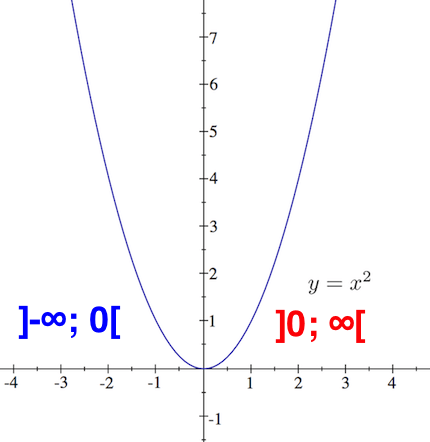
Die Funktion f (x) = x² ist im Intervall
]-∞; 0 [ streng monoton fallend, da f ´ (x) = 2x < 0 für x < 0
]0; ∞ [ streng monoton steigend, da f ´ (x) = 2x > 0 für x > 0
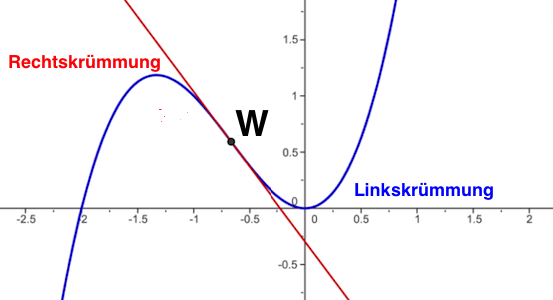
Krümmungsverhalten:
Das Krümmungsverhalten einer Funktion wird mithilfe der 2. Ableitung bestimmt.
f´´ (x) < 0 ⇒ die Funktion ist hier rechtsgekrümmt (konkav).
Sie dreht sich im Uhrzeigersinn.
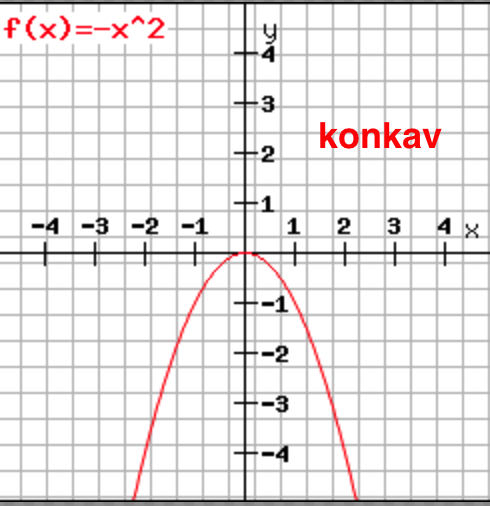
b) Wenn die zweite Ableitung positiv ist, ist die Funktion linksgekrümmt.
f´´ (x) > 0 ⇒ die Funktion ist hier linksgekrümmt (konvex)
Sie dreht sich gegen den Uhrzeigersinn.
Weist eine Funktion Wendepunkte auf, so gibt es Teile mit einer Rechtskrümmung und mit einer Linkskrümmung.