Definition Prismen:
Ein Prisma besteht hinsichtlich seiner Oberfläche aus drei Teilen: Grundfläche, Deckfläche und Mantelfläche.
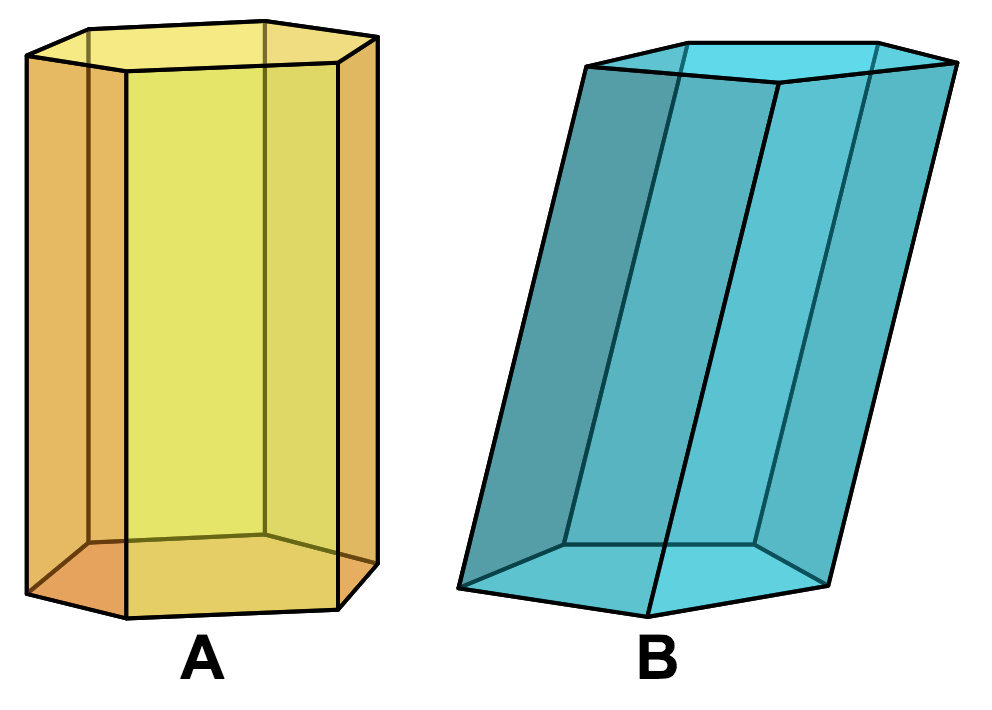
Ein gerades Prisma erhält man, wenn man eine Fläche senkrecht zu seiner Grundfläche parallel verschiebt.
Bei einem schiefen Prisma hingegen stehen die Seitenkanten nicht normal zur Grundfläche.
Eigenschaften eines geraden Prismas:
Die Grundfläche und die Deckfläche bestehen aus jeweils kongruenten Flächen.
Die Grundfläche ist die Fläche, die sich unten befindet.
Die Deckfläche ist die Fläche, die sich oben befindet.
Die Seitenflächen eines Prismas sind Rechtecke.
Die Seitenflächen bilden den Mantel des Prismas.
Je nach Grundfläche unterscheidet man zwischen dreiseitigen, vierseitigen, etc. Prisma
Die Seitenkanten beim Prisma sind gleich lang und parallel.
Der Abstand zwischen den parallelen Flächen gibt die Höhe des Prismas an.
Folgende Formeln sind immer gleich:
Oberfläche: O = 2 • Gf + M
Mantel: M = UG • h
Volumen: V = Gf • h
Masse: m = V • Dichte
Folgende Formeln ändern sich:
a) dreiseitiges Prisma je nach Grundfläche
Grundfläche (Gf) und Umfang der Grundfläche (UG):
Aus dem Flächeninhalt A → Grundfläche Gf
Aus dem Umfang U → Umfang der Grundfläche UG
Rechtwinkliges Dreieck:
Grundfläche:
Gf = a • b : 2
Umfang der Grundfläche:
UG = a + b + c
Gleichschenkliges Dreieck:
Grundfläche:
Gf = c • hc : 2
Gf = a • ha : 2
Umfang der Grundfläche:
UG = 2 • a + c
Gleichseitiges Dreieck:
Grundfläche:
Gf = a² • √3 : 4
Umfang der Grundfläche:
UG = 3 • a
Allgemeines Dreieck:
Grundfläche:
Gf = a • ha : 2
Gf = b • hb : 2
Gf = c • hc : 2
Umfang der Grundfläche:
UG = a + b + c
b) vierseitiges Prisma je nach Grundfläche:
Grundfläche (Gf) und Umfang der Grundfläche (UG):
Aus dem Flächeninhalt A → Grundfläche Gf
Aus dem Umfang U → Umfang der Grundfläche UG
Quadrat:
Grundfläche:
Gf = a²
Umfang der Grundfläche:
UG = 4 • a
Rechteck:
Grundfläche:
Gf = a • b
Umfang der Grundfläche:
UG = 2 • (a + b)
Raute:
Grundfläche:
Gf = a • ha : 2
Gf = e • f : 2
Umfang der Grundfläche:
UG = 4 • a
Parallelogramm:
Grundfläche:
Gf = a • ha : 2
Gf = b • hb : 2
Umfang der Grundfläche:
UG = 2 • (a + b)
Trapez:
Grundfläche:
Gf = (a + c) • h : 2
Umfang der Grundfläche:
UG = a + b + c + d
Formeln für Umkehraufgaben:
Oberfläche: O = 2 • Gf + M
⇒ M = O – 2 • Gf
⇒ Gf = (O – M) : 2
Mantel: M = UG • h
⇒ UG = M : h
⇒ h = M : UG
Volumen: V = Gf • h
⇒ Gf = V : h
Masse: m = V • Dichte
⇒ V = m : Dichte
⇒ Dichte = m : V
Übungsblätter:
Dreiseitige Prismen Übungsblatt
