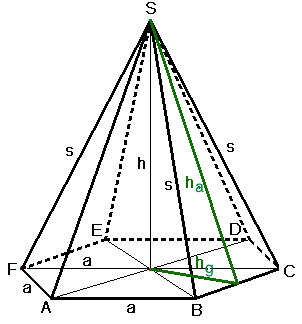
Sechsseitige Pyramide Formelsammlung:
a) Formeln:
Oberfläche allgemein: O = Gf + M
Oberfläche speziell: O = 1,5a • (a √3 + 2ha)
Volumen allgemein: V = Gf • h
3
Volumen speziell: V = a² • √3 • h
2
Mantel: M = a • ha • 6 (sechs gleichschenklige Dreiecke)
2
Mantel gekürzt: M = a • ha • 3
Grundfläche: Gf = 6 • a² • √3 (sechs gleichseitige Dreiecke)
4
Grundfläche gekürzt Gf = 1,5 • a² • √3
b) Pythagoras:
Körperhöhe:
h² = s² – a² oder h² = ha² – hg²
Flächenhöhe des gleichseitigen Dreiecks am Boden:
ha = a/2 • √3
Seitenflächenhöhe:
ha² = hg² + h² oder ha² = s² – (a/2)²
Außenkante:
s² = h² + a² oder s² = ha² + (a/2)²
c) Umkehraufgaben
Oberfläche: O = Gf + M
⇒ M = O – Gf
⇒ Gf = O – M
Volumen: V = Gf • h : 3
⇒ Gf = √(3 • V : h)
⇒ h = 3 • V : Gf
Mantel: M = a • ha • 3
⇒ a = M : ( 3 • ha)
⇒ ha = M : (3 • a)
Grundfläche: Gf = 1,5 • a² • √3
⇒ a = √[(Gf : (1,5 • √3)]